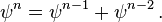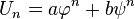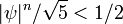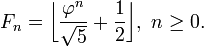Έσπασαν τον κώδικα της υπηρεσιακής πρωθυπουργού

Όπως σωστά παρατήρησε ο @moufanet η υπηρεσιακή πρωθυπουργός φτιάχνει τα μαλλιά της σύμφωνα με την «χρυσή αναλογία» της Σπείρας Fibonacci. Τι ακριβώς σημαίνει όμως αυτό και πως υπολογίζεται πρακτικά;

Όπως διαβάζουμε και στην Βικιπαιδεία «Στα Μαθηματικά, οι Αριθμοί Φιμπονάτσι είναι οι αριθμοί της παρακάτω ακέραιης ακολουθίας: 0,1,1,2,3,5,8,13,21,34,55,89,144, …

Εξ ορισμού, οι πρώτοι δύο αριθμοί Φιμπονάτσι είναι το 0 και το 1, και κάθε επόμενος αριθμός είναι το άθροισμα των δύο προηγούμενων. (αν διαβάσετε το άρθρο της Βικιπαιδείας δώστε προσοχή στο παράδειγμα με τα κουνέλια)

Στην πραγματικότητα βέβαια μια σπείρα Φιμπονάτσι, όπως αυτή που παρατηρείται στα μαλλιά της κα Θάνου, απλώς προσεγγίζει τη λεγόμενη χρυσή σπείρα ή χρυσή αναλογία.

Εάν δεν γνωρίζετε τη συνάφεια με τη Χρυσή Αναλογία παραθέτουμε την παρακάτω πολύ απλή εξήγηση και πάλι από την Βικιπαιδεία:

Έκφραση Κλειστής Μορφής

Όπως κάθε ακολουθία, η οποία προσδιορίζεται από αναδρομική σχέση, έτσι και η ακολουθία Φιμπονάτσι έχει λύση κλειστής μορφής. Αυτή είναι γνωστή ως Φόρμουλα του Binet, αν και ήταν ήδη γνωστό από τον Αβραάμ ντε Μουάβρ

F_n = \frac{\varphi^n-\psi^n}{\varphi-\psi} = \frac{\varphi^n-\psi^n}{\sqrt 5}

όπου

\varphi = \frac{1 + \sqrt{5}}{2} \approx 1.61803\,39887\dots\,

είναι η χρυσή αναλογία, και

\psi = \frac{1 - \sqrt{5}}{2} = 1 - \varphi = - {1 \over \varphi}.

^[11]

Για να το δούμε αυτό,^[12] θα πρέπει το φ και το ψ να είναι και τα δύο λύσεις της εξίσωσης

x^2=x+1,\,x^n=x^{n-1}+x^{n-2},\,

οπότε οι δυνάμει των φ και ψ ικανοποιούν την αναδρομική σχέση Φιμπονάτσι. Δηλαδή

\varphi^n = \varphi^{n-1} + \varphi^{n-2}\,

και

\psi^n = \psi^{n-1} + \psi^{n-2}\, .

Αυτό ισχύει για κάθε τιμή των a και b και η ακολουθία ορίζεται από

U_n=a \varphi^n + b \psi^n

και ικανοποιεί την ίδια αναδρομική σχέση

U_n=a \varphi^{n-1} + b \psi^{n-1} + a \varphi^{n-2} + b \psi^{n-2}=U_{n-1}+U_{n-2}.\,

Εάν a και b επιλεγούν έτσι ώστε U₀ = 0 και U₁ = 1 τότε η ακολουθία U_nπου προκύπτει είναι η ακολουθία Φιμπονάτσι. Αυτό είναι το ίδιο αν απαιτήσουμε τα a και b να ικανοποιούν το παρακάτω σύστημα εξισώσεων: